Penny Jars and Cube Towers

Our Math Workshop emphasis in recent weeks has been centered around analyzing relationships between two quantities in situations of constant change. These situations have started out very concretely, through using actual pennies and linking cubes, and then representing these situations more abstractly with arithmetic expressions.

In the above "penny jar" situation, there is a starting number of 5 pennies in the "jar". Then, 6 pennies are added each "round". The total number of pennies shown is (5 x 6) + 5, or 35 pennies. Students have been challenged to extend patterns such as this one, in order to determine the total number of pennies for any round. If asked to identify the number of pennies in the 20th round, for example, students would determine that there are 20 groups of 6 pennies (20 x 6), and then 5 more (+5) when including the "starting" pennies in the jar: 20 x 6 + 5 = 125. There would be 125 pennies in the jar after 20 rounds of adding 6 pennies each round. The most general arithmetic expression to represent "any" round might be n x 6 + 5, or 6n + 5.

These Investigations (from our Scott Foresman curriculum tool) have provided tables, such as the example shown above, in helping students make sense of (and represent) these situations algebraically.

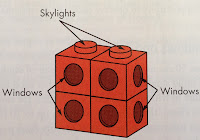
In the above "double tower" situation, there are two skylights. As new "floors" are added to the double tower, the number of skylights never changes. Students have learned to represent this as "+2". Each time a floor is added, however, the double tower gains 6 new windows. The example above has 2 floors. This would be represented as 6 + 6 + 2, or 2 x 6 + 2. There are a total of 14 windows on this tower. Again, students have learned through active exploration (by actually constructing various towers with linking cube manipulatives as they fill in provided charts) how to represent this situation with a general arithmetic expression: n x 6 + 2 (6n + 2). How many windows would be on the 100th floor of this tower? To solve, students would simply calculate 100 x 6 + 2. A 100 floor double tower would have 602 windows.


Upcoming investigations will include building, analyzing, and representing Corner Towers & Square Towers. Students will be challenged to represent these situations of constant change by creating an arithmetic expression using a variable so that the number of windows on ANY given floor can quickly be determined.






Happy Mathematizing,