This method is important because it draws upon important ideas in multiplication (the inverse operation of division). Did you know that multiplication is also referred to as "repeated" addition? Well, division is also referred to as "repeated" subtraction.
635 is the DIVIDEND of a division problem. It represents the TOTAL.
15 is the DIVISOR.
In this division problem, the question we are trying to answer is "How many groups of 15 are in 635?"
This leads us to think of multiplication to help us find the number of groups of 15 that can be made with a total of 635. Since division is repeated subtraction, we must subtract away groups of 15 until we no longer have enough left to make another group of 15.
A brainstorming process happens next. Because 635, is so much more than 15, we don't want to take away only a few groups of 15 at a time. The goal is to work as efficiently as possible.
We know that 1 x 15 is equal to 15, therefore 10 groups of 15 (10 x 15) is equal to 150. Working with landmark multiples of 10 (10, 20, 30, 40) is important and is built from our knowledge of basic multiplication facts.
Notice that this brainstorming process has helped to determine that 40 groups of 15 is equal to 600. (This is close to our total of 635.) Using this problem helps us to "take away" (repeated subtraction) 40 groups of 15 from the 635 total, and this leaves only a difference of 35.
Then, taking away another 2 groups of 15 (2 x 15), leaves a final difference of 5 (which is the "remainder" as 5 is not enough to make another group of 15).
This work shows that 42 groups of 15 can be made (or subtracted away) from 635 and that there will be 5 left over. It is very helpful to represent this remainder as a fraction since we are left with "part" of a new group of 15 and the fraction helps us to understand that this is what the remainder (left-over) means.
42 groups of 15 were made and we have "5/15" or "1/3" of a another group.
The above example has shown the most efficient way to subtract groups of 15 (40 groups and then 2 groups), however, students may solve this problem in many different ways. Below shows another example of how the Partial Quotients method might be used to solve this same problem.
You will notice that 42 groups of 15 were still subtracted, but the process occurred in four steps instead of two steps.
In addition to this strategy, there are other division strategies students use to solve division problems. Page 9 in the student planners highlight a few of these strategies (such as use of a multiple tower or ratio table/skip counting).
This Partial Quotients method will be a preferred method as we progress through the 4th grade as it connects with the traditional algorithm for division, which is a major focus in 5th grade.
Happy Mathematizing!



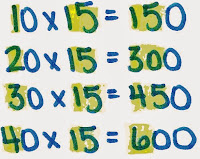



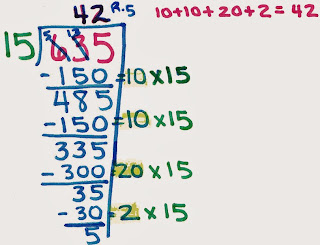

I'm so glad my kids are learning to be the kind of mathematician I never got to be in my years of elementary!
ReplyDeleteThis is my go to division strategy.I love using it because it is so efficient!
ReplyDelete